In [1]:
# To support both python 2 and python 3
from __future__ import division, print_function, unicode_literals

# Common imports
import numpy as np
import os

# to make this notebook's output stable across runs
np.random.seed(42)

# To plot pretty figures
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12

和 svm 一样，决策树是一种多功能机器学习算法，即可以执行分类任务也可以执行回归任务，甚至包括多输出任务。

它可以对很复杂的数据集进行拟合。是随机森林的基本组成部分，而随机森林是当今最强大的机器学习算法之一。

这里我们将讨论决策树的训练、可视化、预测。

然后学习 sklearn 上使用 cart 算法，并讨论如何调整决策树让他可以用于执行回归任务。

最后，讨论决策树目前的一些局限性。

In [5]:
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, 2:]
y = iris.target
# 构造决策树
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
Out[5]:
DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=2,
            max_features=None, max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, presort=False, random_state=42,
            splitter='best')
In [17]:
# 我们可以使用 export_graphviz 方法，生成一个叫做 iris_tree.dat 的图形定义文件来
# 将一个训练好的决策树模型进行可视化。
from sklearn.tree import export_graphviz
export_graphviz(
    tree_clf,
    out_file = os.path.join('.', 'images', 'decision_trees', 'iris_tree.dot'),
    feature_names = iris.feature_names[2:],
    class_names = iris.target_names,
    rounded = True,
    filled = True
)
# 执行以下指令即可将 dot 文件转换成 png 文件显示了
# dot -Tpng iris_tree.dot -o iris_tree.png

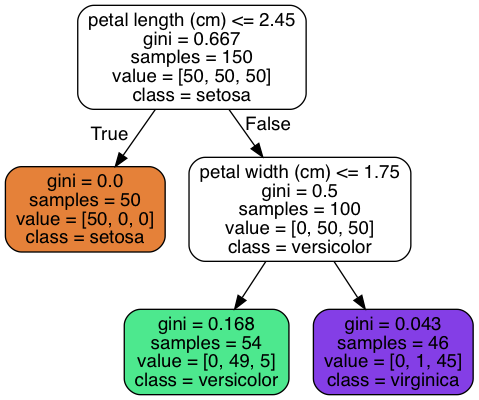
cover

开始预测

我们来解读一下上图，假设我们找到一朵鸢尾花并且想对它进行分类，那么我们从根节点开始：该节点判断花瓣长度是否小于 2.45 。如果是，那么它是唯一的结果， Iris-Setosa 。如果是，它继续询问，花瓣的宽度是否小于 1.75 。如果是，它是 Iris-Versicolor 。如果不是，它是 Iris-Virginica 。

这很简单，对吧。决策树的众多特性之一就是，它不需要进行特征缩放或者归一化，它不需要太多的数据预处理。

节点的 samples 属性统计了有多少样本属于本实例。

节点的 value 属性记录了每一个类别的样例有多少个。比如说右下角的节点，包含 0 个 setosa ， 1 个 versicolor ， 1 个 virginica 。

节点的 gini 属性测量了它的纯度：如果一个节点包含的所有训练样例全部都是同一类别的，也就是说这个样例his纯的 ( gini = 0 ) 。其计算公式：

$$G_{i}=1-\sum_{k=1}^{n}P_{i,k}^{2}$$

p(i,k) 表示第 i 个节点中训练样例为第 k 类的比例。

所以深度为 2 的左侧的节点的 gini = 1 - (0/54)^2 - (49/54)^2 - (5/54)^2 = 0.168

sklearn 使用的是 cart 算法， cart 算法仅产生二叉树：每一个非叶节点总是只有两个子节点（只有是或否两个结果）。然而像 ID3 这样的算法可以产生超过两个子节点的决策树模型。

In [21]:
from matplotlib.colors import ListedColormap

def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
    x1s = np.linspace(axes[0], axes[1], 100)
    x2s = np.linspace(axes[2], axes[3], 100)
    x1, x2 = np.meshgrid(x1s, x2s)
    # 网格
    X_new = np.c_[x1.ravel(), x2.ravel()]
    y_pred = clf.predict(X_new).reshape(x1.shape)
    custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
    plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
    if not iris:
        custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
        plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
    if plot_training:
        plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
        plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
        plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris-Virginica")
        plt.axis(axes)
    if iris:
        plt.xlabel("Petal length", fontsize=14)
        plt.ylabel("Petal width", fontsize=14)
    else:
        plt.xlabel(r"$x_1$", fontsize=18)
        plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
    if legend:
        plt.legend(loc="lower right", fontsize=14)

plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf, X, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.80, "Depth=1", fontsize=13)
plt.text(4.05, 0.5, "(Depth=2)", fontsize=11)
plt.show()

上图显示了决策树的决策边界。粗的垂直线代表了根节点 ( 深度为 0 ) 的决定边界：花瓣长度为 2.45 cm 。由于左侧区域是纯的 ( 只有 Iris-Setosa ) ，所以不能再进一步分裂。然而，右边的区域不是纯的，所有深度为 1 的右节点在花瓣宽度为 1.75 cm 处分裂。如果设置 max_depth 为 3 ，每一个深度为 2 的节点，都会添加一个决策边界。

可以发现，决策树非常直观，它的决定也很容易被解释，这种模型通常被称为白盒模型。相反，随机森林或神经网络通常被认为是黑盒模型。他们能做出很好地预测，并且你可以轻松检查他们做出这些预测过程中计算的执行过程。然而，人们通常很难用简单的属于来解释为什么模型做出这样的预测。

估计分类概率

决策树还可以估计某个实例属于特定类 k 的概率：首先遍历树来查找实例的叶节点，然后它返回此节点中类 k 的训练实例的比例。

例如，我们发现一个花瓣长为 5cm ，宽为 1.5cm 的花朵。相应的叶节点是深度为 2 的左节点，因此决策树应该输出以下概率：

  • iris-setosa: 0/54
  • iris-versicolor: 49/54
  • iris-virginica: 5/54

如果是具体的类，它应该输出 iris-versicolor (类别1)，因为它具有最高的概率。

cover

In [22]:
tree_clf.predict_proba([[5, 1.5]])
Out[22]:
array([[0.        , 0.90740741, 0.09259259]])
In [23]:
tree_clf.predict([[5, 1.5]])
Out[23]:
array([1])

CART 训练算法

sklearn 用分裂回归树 classification and regression tree 简称 cart 算法，训练决策树，这种思想非常简单：

首先使用单个特征 k 和阈值 t_k 将训练集分成两个子集。它如何选择 k 和 t_k 呢？它寻找到能够产生最纯粹的子集对 (k, t_k) ，然后通过子集大小加权计算。

算法会尝试使用最小成本函数：

$$J(k,t_{k})=\frac{m_{left}}{m}G_{left}+\frac{m_{right}}{m}G_{right}$$

m 代表样例数， g 代表不纯度

当它成功将训练集分成两部分以后，将继续使用同样的递归式分割子集，然后是子集的子集。

cart 算法是一种贪心算法，它每次寻找最佳的分割，不检查分割是否能够在几个级别中全部可能中找到最佳方法。它不保证全局最优。

不幸的是，找到一个最优树是一个 np 问题，它需要 O(exp(m)) 的时间，即使对于非常小的训练集也会变得棘手。这就是我们为什么必须设置一个合理的解决方案而不是最佳的解决方案。

gini 不纯度

通常，算法使用 gini 不纯度来进行检测，但是也可以通过将标准超参数设置成 'entropy' 来使用熵不纯度来进行检测。这里熵的概念是源于热力学中分子混乱程度的概念，当分子井然有序的时候，熵值接近 0 。

在机器学习中，熵经常被用作不纯度的衡量方式，当一个集合内只含有一类实例时，我们称为数据集的熵为 0 。

熵的减少被称为信息增益。

下面的公式显示了第 i 个节点的熵的定义：

$$H_{i}=-\sum_{k=1,P_{i,k}≠0}^{n}P_{i,k}log(p_{i,k})$$

比如深度为 2 的左节点的熵：

$$-49/54log(49/52)-5/54log(5/54)=0.31$$

所以我们到底是使用 Gini 指数还是熵呢？事实上大部分情况都没有多大的差别，他们会生成类似的决策树。

gini 指数计算稍微快一点，所以这是一个很好地默认值，但是，也有的时候他们会产生不同的树， gini 指数趋向于将在树的分支中将最多的类隔离出来，而熵指数趋向于产生略微平衡一些的决策树模型。

正则化超参数

决策树几乎不对训练数据做任何假设，如果不添加约束，树结构模型通常将根据训练数据调整自己，使自身能够很好的拟合数据，而这种情况下大多数会导致模型过拟合。

这一类模型被称作非参数模型，不是因为它没有任何参数，而是因为在训练之前没有确定参数的具体数量，像线性回归这样的参数模型是有事先设定好的参数数量，所以自由度是受限的，这就减少了过拟合的风险。

DesicionTreeClassifier 类还有一些其他参数用于限制树模型的形状。

  • min_samples_splot : 节点在被分裂之前必须具有的最小样本数
  • min_samples_leaf : 叶节点必须具有的最小样本数
  • min_weight_fraction_leaf : 和 min_samples_leaf 相同，但表示为加权总数的一小部分实例
  • max_leaf_nodes : 叶节点的最大数量
  • max_features : 在每个节点被评估是否分裂的时候，具有的最大特征数量

一些其他算法的工作原理是在没有任何约束条件下训练决策树模型，让模型自由生长，然后再对不需要的节点进行剪枝。

当一个节点的全部子节点都是叶节点时，如果它对纯度的提升不具有统计学意义，我们就认为这个节点是不必要的。

标准的假设检验，例如卡方检测，通常会被评估一个概率值——即改进是够纯粹是偶然性的结果。

如果 p 值比给定的阈值更高，那么节点被认为是非必要的，它的子节点会被删除。

In [97]:
# 我们现在用 moons 数据集来生成决策树模型，首先使用默认超参数生成
from sklearn.datasets import make_moons
Xm, ym = make_moons(n_samples=100, noise=0.25, random_state=53)

deep_tree_clf1 = DecisionTreeClassifier(random_state=42)
deep_tree_clf1.fit(Xm, ym)
plot_decision_boundary(deep_tree_clf1, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("No restrictions", fontsize=16)
plt.show()
In [96]:
# 上面的模型过拟合了，我们设置 min_samples_leaf = 4
# 叶节点必须具有的最小样本数
# 与之对比，我们再生成一个
deep_tree_clf2  = DecisionTreeClassifier(random_state=42, min_samples_leaf=4)
deep_tree_clf2.fit(Xm, ym)
plot_decision_boundary(deep_tree_clf2, Xm, ym, axes=[-1.5, 2.5, -1, 1.5], iris=False)
plt.title("min_samples_leaf = {}".format(deep_tree_clf2.min_samples_leaf), fontsize=14)
plt.show()

回归

我们之前提到过，决策树也能进行回归任务，让我们用 sklearn 的 DecisionTreeRegressor 类构建一个回归树，让我们用 max_depth = 2 在具有噪声的二次项数据集上进行训练。

In [125]:
from sklearn.tree import DecisionTreeRegressor
# Quadratic training set + noise
np.random.seed(42)
m = 200
X = np.random.rand(m, 1)
y = 4 * (X - 0.5) ** 2
y = y + np.random.randn(m, 1) / 10
tree_reg = DecisionTreeRegressor(max_depth=2)
tree_reg.fit(X, y)
Out[125]:
DecisionTreeRegressor(criterion='mse', max_depth=2, max_features=None,
           max_leaf_nodes=None, min_impurity_decrease=0.0,
           min_impurity_split=None, min_samples_leaf=1,
           min_samples_split=2, min_weight_fraction_leaf=0.0,
           presort=False, random_state=None, splitter='best')
In [127]:
export_graphviz(
    tree_reg,
    out_file = os.path.join('.', 'images', 'decision_trees', 'tree_reg.dot'),
    rounded = True,
    filled = True
)
# dot -Tpng tree_reg.dot -o tree_reg.png

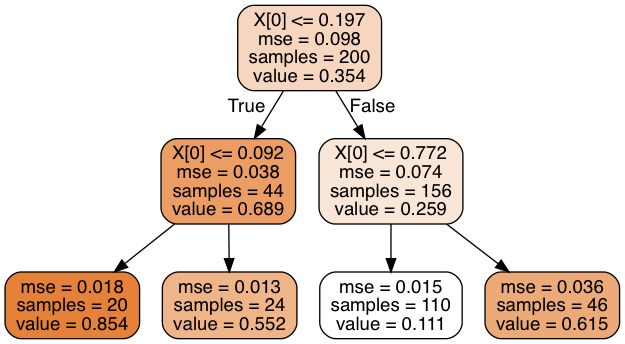
cover

它和之前建立的分类树很像，他们的主要区别在于，它不是预测每个节点中的样本的所属分类，而是预测一个具体的数值，例如，我们想对 x1=0.6 的新实例进行预测，从根开始遍历树，最终到达预测值等于 0.1106 的叶节点。该预测值为 0.11 的叶节点，该预测仅仅是与该叶节点相关的110个训练实例的平均目标值，而这个预测结果在对应的110个实例上的均方误差 MSE 等于0.0151

In [135]:
from sklearn.tree import DecisionTreeRegressor
tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg1.fit(X, y)

def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"):
    x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
    y_pred = tree_reg.predict(x1)
    plt.axis(axes)
    plt.xlabel("$x_1$", fontsize=18)
    if ylabel:
        plt.ylabel(ylabel, fontsize=18, rotation=0)
    plt.plot(X, y, "b.")
    plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")

plot_regression_predictions(tree_reg1, X, y)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
    plt.plot([split, split], [-0.2, 1], style, linewidth=2)
plt.text(0.21, 0.65, "Depth=0", fontsize=15)
plt.text(0.01, 0.2, "Depth=1", fontsize=13)
plt.text(0.65, 0.8, "Depth=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)
plt.show()
# 这里我们仅仅设置了 max_depth = 2 ，如果设置为 3 ，图像将进一步变化。
# 同时注意到每个区域的预测值总是该区域中实例的平均目标值。
In [134]:
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg2.fit(X, y)

plot_regression_predictions(tree_reg2, X, y, ylabel=None)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
    plt.plot([split, split], [-0.2, 1], style, linewidth=2)
for split in (0.0458, 0.1298, 0.2873, 0.9040):
    plt.plot([split, split], [-0.2, 1], "k:", linewidth=1)
plt.text(0.3, 0.5, "Depth=2", fontsize=13)
plt.title("max_depth=3", fontsize=14)
plt.show()
# 算法以一种使大多数训练实例尽可能接近该预测值的方式分割每个区域。

cover

CART 算法的工作方式与之前处理分类模型基本一样，不同之处在于现在不再以最小化不纯度的方式分割数据集，而是试图以最小化 MSE 的方式分割训练集。

$$J(k,t_{k})=\frac{m_{left}}{m}MSE_{left}+\frac{m_{right}}{m}MSE_{right} where\left\{\begin{matrix}MSE_{node}=\sum_{i∈node}(\widehat{y}_{node}-y^{i})^{2} \\ \widehat{y}_{node}=\frac{1}{m_{node}}\sum_{i∈node}y^{(i)} \end{matrix}\right.$$

和之前一样，m 代表数量，这里的改变在于 将 gini 改成了 mse。

决策树在处理回归问题的时候也会过拟合，如果不添加任何正则化，我们可能会过度拟合，而我们设置了比如 min_samples_leaf 这样的参数，结果会好很多。

In [138]:
# 过拟合
tree_reg1 = DecisionTreeRegressor(random_state=42)
tree_reg1.fit(X, y)
x1 = np.linspace(0, 1, 500).reshape(-1, 1)
y_pred1 = tree_reg1.predict(x1)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", fontsize=18, rotation=0)
plt.legend(loc="upper center", fontsize=18)
plt.title("No restrictions", fontsize=14)
Out[138]:
Text(0.5,1,'No restrictions')
In [139]:
# 设置超参数，效果好了很多
tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)
tree_reg2.fit(X, y)
y_pred2 = tree_reg2.predict(x1)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred2, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.title("min_samples_leaf={}".format(tree_reg2.min_samples_leaf), fontsize=14)
plt.show()

不稳定性

我们了解到决策树有哪些特点呢？

它很容易理解和解释，易于使用且功能丰富而强大，然而，它有一些限制，我们喜欢设定正交化的决策边界，这使得它对训练集的旋转敏感。如果我们将输入数据进行一定的旋转，那么决策树的边界看起来会格外复杂。

解决这个问题将使用 PCA 主成分分析方法，这样通常会让训练结果变得好一些。

更加通俗的讲，决策时的主要问题是它对训练数据的微小变化非常敏感，即使使用相同的训练数据，我们可能也会得到差别很大的模型。

随机森林可以通过多棵树的平均预测值限制这种不稳定性。